Calculus 14: n’th Derivative with % (modulo) & sympy

1. n’th derivatives of \(\cos{x}\)

• Find first few derivatives of: \[\cos(x)\]

• Look for a pattern, then find: \[\frac{d^{99}}{dx^{99}}\cos(x)\]

2. Hand-Written Solution

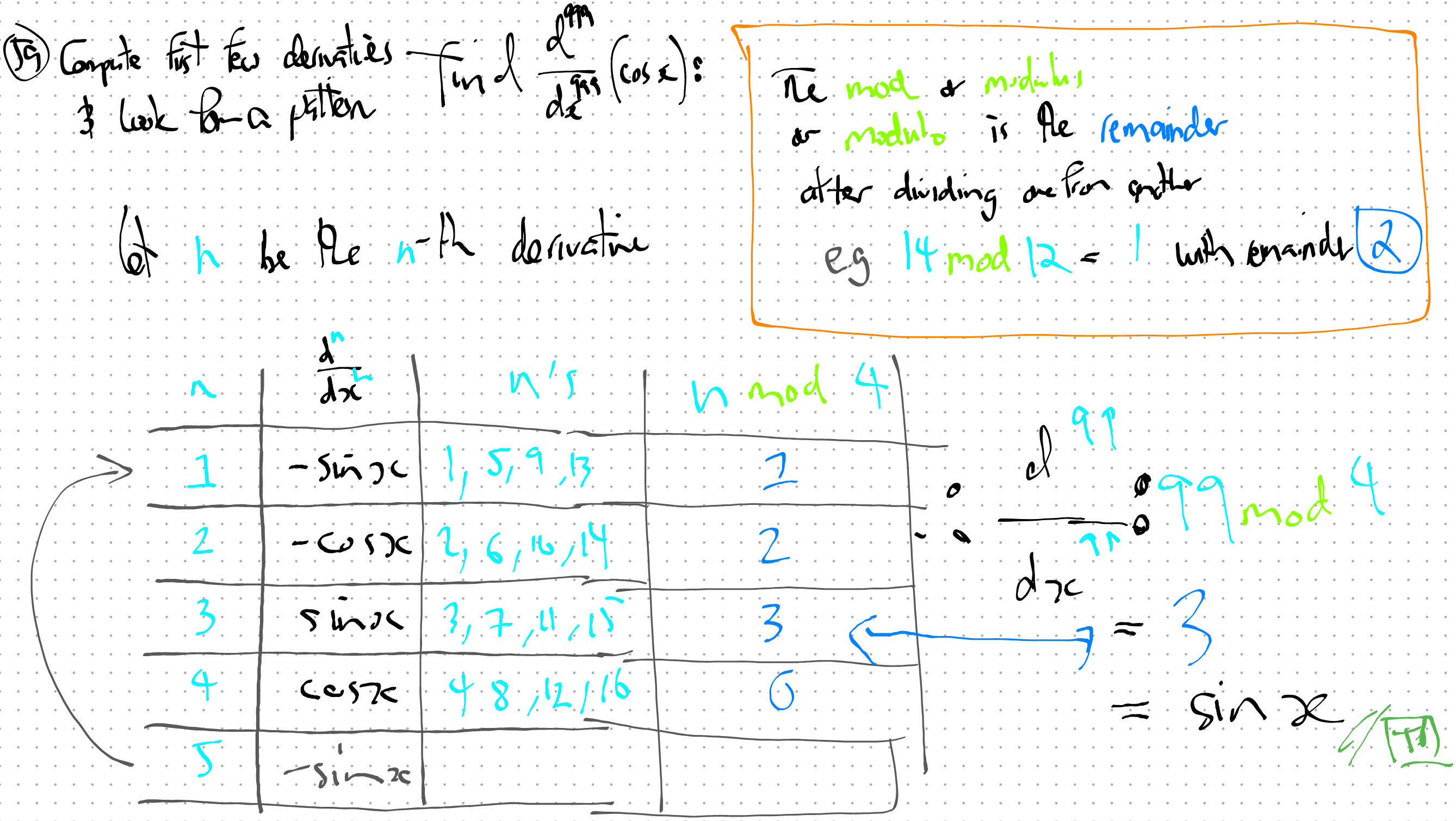
3. Validating n’th Derivative - Modulus 4 (Python)

for i in range(10):
    print(f"{i}mod4: {i%4}")

0mod4: 0
1mod4: 1
2mod4: 2
3mod4: 3
4mod4: 0
5mod4: 1
6mod4: 2
7mod4: 3
8mod4: 0
9mod4: 1

4. Validating n’th Derivative - sympy

import sympy as sp
x = sp.Symbol('x')
print(x,type(x))
# sp.diff(sp.sin(x), x)
# sp.diff(sp.sin(x), x,1)
# sp.diff(sp.sin(x), x,2)
# sp.diff(sp.cos(x), x,3)
for i in range(1,6):
    print(f"ddx{i}(cosx): {sp.diff(sp.cos(x), x,i)}")

x <class 'sympy.core.symbol.Symbol'>
ddx1(cosx): -sin(x)
ddx2(cosx): -cos(x)
ddx3(cosx): sin(x)
ddx4(cosx): cos(x)
ddx5(cosx): -sin(x)

5. Solution - sympy

\(\frac{d^{99}}{dx^{99}}\cos{x}\)

x = sp.Symbol('x')
print(f"ddx{99}(cosx): {sp.diff(sp.cos(x), x,99)}")

ddx99(cosx): sin(x)