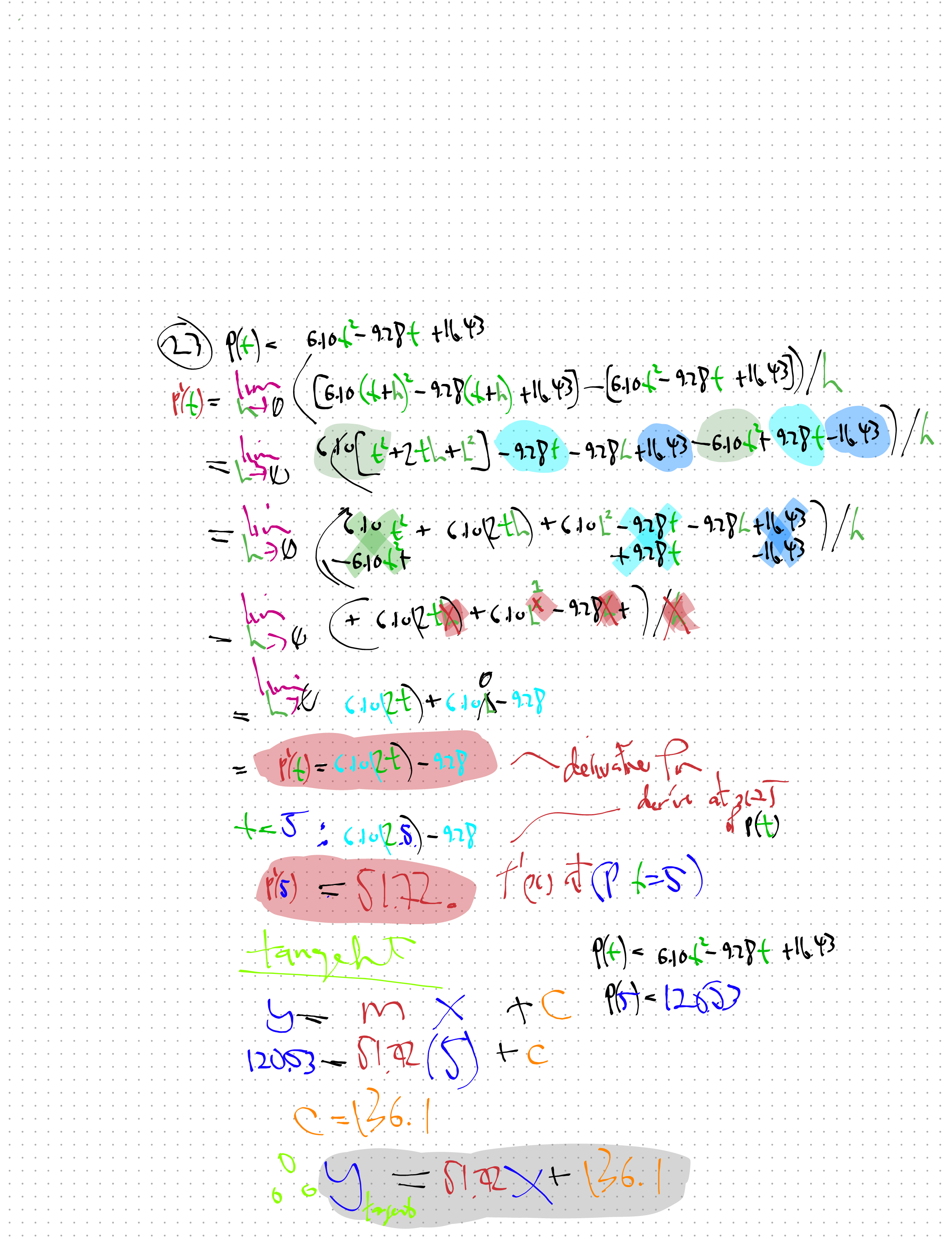\(f(x)=6t^2-9.28t+16.43\)

Find \(f'(t)\) at \(t=5\)

1. Working-Out (Hand-written)

from matplotlib.ticker import MaxNLocator
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

xpt = 5
x_deviation = 2
x_increments = 21
xs_min = xpt - x_deviation
xs_max = xpt + x_deviation
xs = np.linspace(xs_min, xs_max, x_increments)  # XS
# # X-EXCLUDE LIMIT VALUE
# xs = xs[xs != 1]
# xs = xs[xs >= 0]

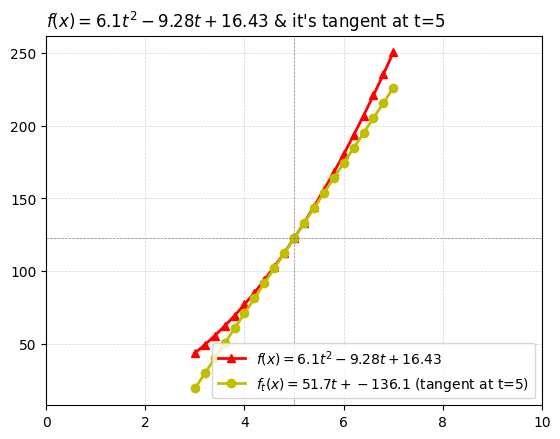
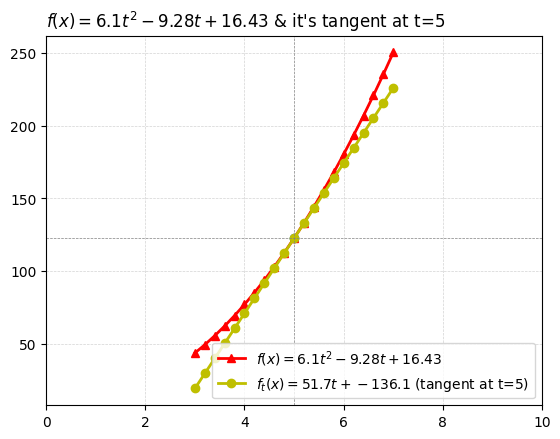
lbl_numerator = r'$f(x)= 6.1t^{2}-9.28t+16.43$'   # LABEL
fx_numerator = lambda x: 6.1*(x**2)-9.28*x+16.43   # F(X)
ys_numerator = fx_numerator(xs)             # YS = F(XS) 
ypt_fx = fx_numerator(xpt)
print(f"ypt_fx_at_P(x={xpt}): {ypt_fx}")
# lbl_denom = r'$f(x)=x-2$'
# fx_denom = lambda x: x-2
# ys_denom = fx_denom(xs)

lbl_dydx = r"$f'(x)=6.10*(2t)-9.28$ (dydx or slope fn)"
fx_dydx = lambda x: 6.1*(2*x)-9.28
xpt_dydx = xpt
dydx = fx_dydx(xpt_dydx)
print(f"ypt_dydx_at_P(x={xpt_dydx}): {dydx}")

c_tangent = ypt_fx-(dydx)*(xpt)
tgt = "tangent"
lbl_tangent = rf'$f_t(x)={dydx:,.1f}t+{c_tangent:,.1f}$ (tangent at t={xpt})'
fx_tangent = lambda x: dydx*xs+c_tangent
ys_tangent = fx_tangent(xs)


plot_title = lbl_numerator + f" & it's tangent at t={xpt}"
# plot_title = lbl_numerator + "at (4,2)"
# plot_title = lbl_denom + " and " + lbl_denom + "at (3,3)"
# plot_title = lbl_numerator + " and " + lbl_tangent + "at (4,2)"

plt.plot(xs, ys_numerator,  'r^-', linewidth=2, markersize=6, label=lbl_numerator)
# plt.scatter(xs, ys_numerator, marker="o")
# plt.plot(xs, ys_denom,      'bo-', linewidth=2, markersize=8, label=lbl_denom)
plt.plot(xs, ys_tangent,      'yo-', linewidth=2, markersize=6, label=lbl_tangent)

# zoom and enhance!
plt.xlim(xpt-5,xpt+5)  # X-axis range
# plt.ylim(-0.1, 0.1)  # Y-axis range

# Add grid, title, and legend
plt.grid(color='lightgrey', linestyle='--', linewidth=0.5)
plt.title(plot_title, loc='left')
# plt.title(r"$12*x+16$", loc='left')
# plt.legend(loc='upper right')
plt.legend(loc='lower right')

# Optionally, add vertical and horizontal lines to highlight the zoomed area
ax = plt.gca()  # Get the current axis
ax.axvline(x=xpt, color='grey', linestyle='--', linewidth=0.5)
ax.axhline(y=fx_numerator(xpt), color='grey', linestyle='--', linewidth=0.5)

plt.scatter(x=xpt, y=fx_numerator(xpt), marker="o")
# print(fx_numerator(5))

ypt_fx_at_P(x=5): 122.53
ypt_dydx_at_P(x=5): 51.72

# # X-LIMIT & VALUE
# plt.vlines(x_at_c,linestyles="dotted", ymin=plt.ylim()[0], ymax=max(ys)) # non-monotonic
# # plt.plot(x_at_c, 0.5,marker="o",markersize=15, markerfacecolor='none', markeredgecolor='red')

# # OTHER
# # # b+-- , o:b , r^ , bo    plt.xlabel("") 
# # plt.ylim(bottom=0)  # chart starts from y=0
# # ax.yaxis.set_minor_locator(ticker.MultipleLocator(0.000025)) # minor ticks
# # ref: https://matplotlib.org/stable/users/explain/axes/axes_ticks.html