import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
xs = np.linspace(-0.1,0.1,20)
xs = xs[xs != 0] # remove x=0
def f(x): return (x)/(np.abs(x))
ys = f(xs)
plt.scatter(xs,ys)
plt.grid(True)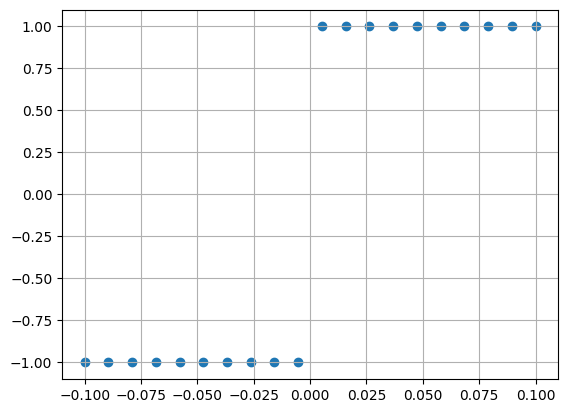
Tony Phung
December 19, 2024
import numpy as np
import matplotlib.pyplot as plt
x_at_c = 2
abt_c = 0.1
xs_min = x_at_c - abt_c
xs_max = x_at_c + abt_c
xs = np.linspace(xs_min,xs_max,20)
def fx(x): return (2*x+5)/(11-x**3)
ys = fx(xs)
plt.scatter(xs, ys, marker="+")
plt.grid(True)
plt.vlines(x=x_at_c,linestyles="dotted", ymax=fx(xs_max),ymin=fx(xs_min))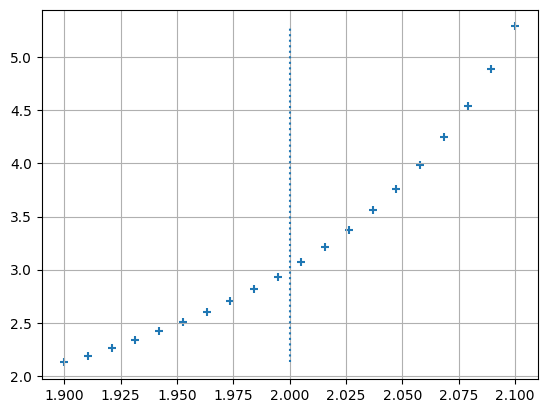
import numpy as np
import matplotlib.pyplot as plt
x_at_c = -3
abt_c = 0.1
xs_min = x_at_c - abt_c
xs_max = x_at_c + abt_c
xs = np.linspace(xs_min,xs_max,20)
def fx(x): return (5-x)**(4/3)
ys = fx(xs)
plt.scatter(xs, ys, marker="+")
plt.grid(True)
plt.vlines(x=x_at_c,linestyles="dotted", ymax=fx(xs_max),ymin=fx(xs_min))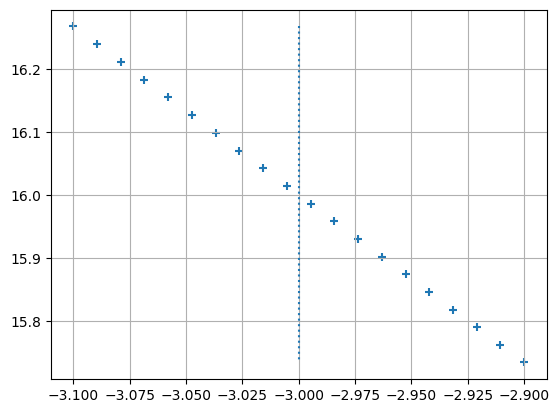
import numpy as np
import matplotlib.pyplot as plt
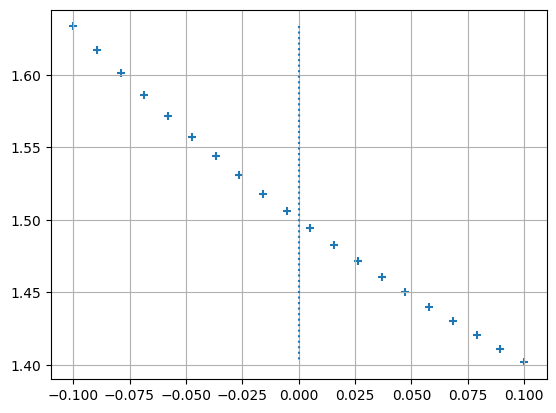
x_at_c = 0
abt_c = 0.1
xs_min = x_at_c - abt_c
xs_max = x_at_c + abt_c
xs = np.linspace(xs_min,xs_max,20)
def fx(x): return 3/(np.sqrt(3*x+1)+1)
ys = fx(xs)
plt.scatter(xs, ys, marker="+")
plt.grid(True)
plt.vlines(x=x_at_c,linestyles="dotted", ymax=fx(xs_max),ymin=fx(xs_min))