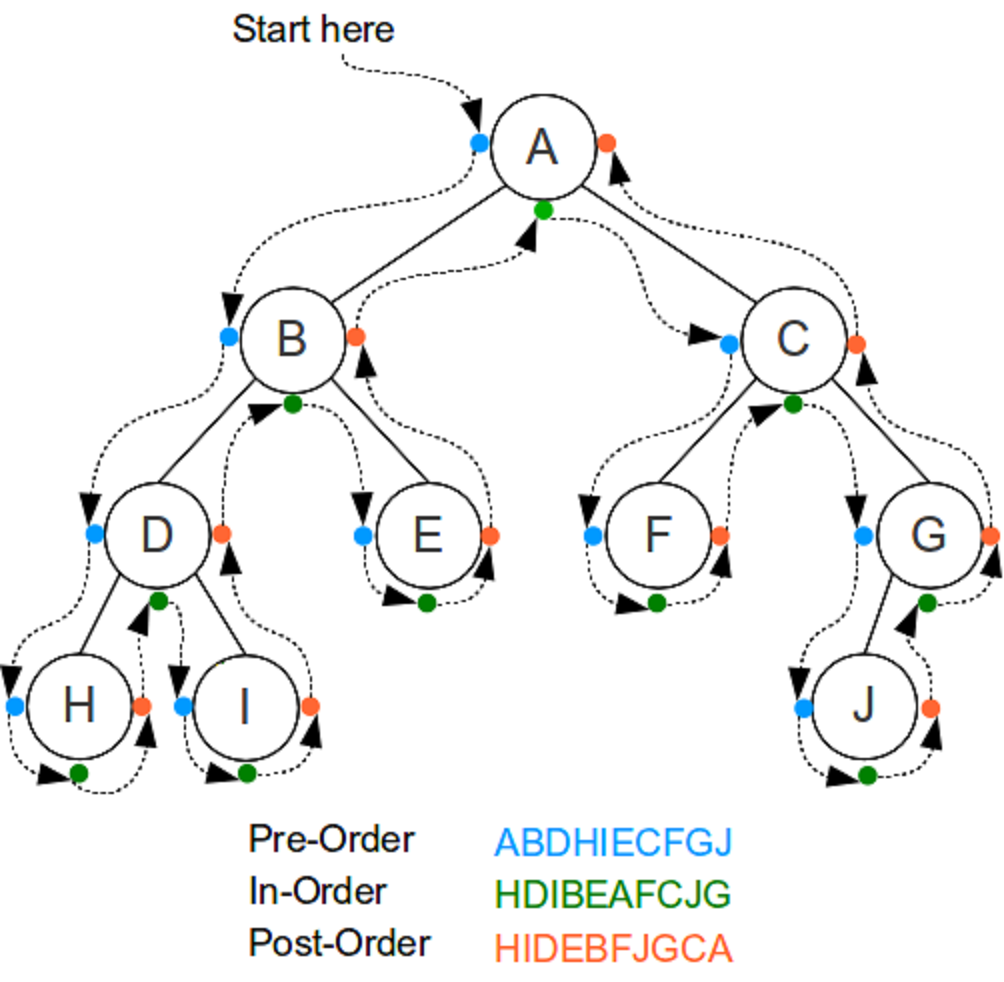
1. Draw a BST

Insert into a empty BST the folloowing in this order:

[1, 5, 9, 2, 4, 10, 6, 3, 8].

Draw a diagram showing what the BST

1.1 Draw a BST: Tony’s Solution

2. `Search`: BST

Find maximum number of steps to search value in Balanced BST with 1,000 values.

2.1 `Search`: BST - Tony’s Solution

Searching() value in BST is \(\log_2(n)\):
\[steps = \log_2(n)=\log_2(1000)\]

Apply change of base formula:

\[\log_2(1000) = \frac{\log_{10}1000}{\log_{10}2}\]

\[log_{10}1000 = 3\] \[log_{10}2=0.301\]

\[\log_2(1000) = \frac{3}{0.301}\]
\[\approx 9.97\] \[or\ 10\ steps\]

3. `max()` Value in BST - Tony’s Solution

Write the algorithm to find node with greatest value in BST.

3.1. `TreeNode` & `insert_node`: Setup

Introduced previously.

class TreeNode: #4 mins
    def __init__(self,data,left=None,right=None):
        self.data=data
        self.left=left
        self.right=right
        
def insert_node(root_node: TreeNode, target: int):
    current_node = root_node
    
    if current_node.data == target:
        print(f"t{target}==c{current_node.data}: cant insert duplicates")
        return current_node.data
    elif target < current_node.data:
        print(f"t{target}<-c{current_node.data}: go left")
        if current_node.left:
            current_node = current_node.left
            return insert_node(current_node, target)
        else:  
            print(f"t{target}<-c{current_node.data}: no left_child insert left of c[{current_node.data}]")
            current_node.left = TreeNode(target)
            return current_node.left
    else:
        print(f"t{target}->c{current_node.data}: go right")
        if current_node.right:
            current_node = current_node.right
            return insert_node(current_node, target)
        else:  
            print(f"t{target}->c{current_node.data}: no right_child insert right of c[{current_node.data}]")
            current_node.right = TreeNode(target)
            return current_node.right

def insert_node_clean(root_node: TreeNode, target: int):
    current_node = root_node
    
    if current_node.data == target:
        # print(f"t{target}==c{current_node.data}: cant insert duplicates")
        return current_node.data
    elif target < current_node.data:
        # print(f"t{target}<-c{current_node.data}: go left")
        if current_node.left:
            current_node = current_node.left
            return insert_node_clean(current_node, target)
        else:  
            # print(f"t{target}<-c{current_node.data}: no left_child insert left of c[{current_node.data}]")
            current_node.left = TreeNode(target)
            return current_node.left
    else:
        # print(f"t{target}->c{current_node.data}: go right")
        if current_node.right:
            current_node = current_node.right
            return insert_node_clean(current_node, target)
        else:  
            # print(f"t{target}->c{current_node.data}: no right_child insert right of c[{current_node.data}]")
            current_node.right = TreeNode(target)
            return current_node.right
        
        
        
def insert_from_list(root, node_list: list[int], show_results:bool = False):
    for node in node_list:
        if show_results:
            insert_node(root, node)
            print()
        else:
            insert_node_clean(root, node)

3.2 `traverse()`

def traverse(root_node: TreeNode):
    if not root_node:
        return
    traverse(root_node.left)
    print(root_node.data)
    traverse(root_node.right)
    
root = TreeNode(50)
insert_from_list(root, [25,75,10,35,25])
traverse(root)

3.3 `find_max()` Value in BST - Tony’s Solution

def find_max(root_node: TreeNode):
    if not root_node:
        return
    while root_node.right:
        return find_max(root_node.right)
    return root_node.data


root = TreeNode(50)
insert_from_list(root, [25,75])
find_max(root)

# PSUEDO

#  50 
# 25  75

# [ENTERED]find_max{ [root_node==TreeNode(50)]}:
# - [enter] while-loop: [c.r][75] exists: ---> recurse find_max{[c.r][75]}:
#   - [ENTERED]find_max{ root_node.right=TreeNode(75) }:  
#     - [enter] while-loop: [c.r][N] DOES NOT exists
#     - [return] c.data=75
#   - [RETURND]{find_max{ ret[75] }
# - [exitd] while-loop: ret[75] <--- from find_max{ TreeNode(75) }
# [return] ret[75]

3.4 `find_max()` Version 2 - Tony’s Solution

def GET_MAX(root_node: TreeNode):
    if not root_node:
        return
    while root_node.right:
        return GET_MAX(root_node.right) # this is hit at every level down and up
    return root_node.data # this is only hit once

root = TreeNode(50)
insert_from_list(root, [25,75,80])
GET_MAX(root)


#  50 
# 25  75
#       80

# PSUEDO CODE
# [ENTERED]GET_MAX{ [rn=TreeNode(50)]}:
# - (50)[enter] while-loop: [c.r][50.75] YES exists: 
# - (50)[enter] GET_MAX{[c.r][50.75]}:
#   - (75)[ENTERED] {GET_MAX{  rn==TN(75) }:  
#   - (75)[enter] while-loop: [c.r][50.75.80] YES exists: 
#   - (75)[enter] GET_MAX{[c.r][50.75.80]}:
#       - (80)[ENTERED] {GET_MAX{ rn=TN(80) }:  
#       - (80)[skipped] while-loop: [c.r][50.75.80.N] NO xists:
#       - (80)[return] c.data=80 (~ return root_node.data)
#       - (80)[EXITTED] {GET_MAX{ rn=TN(80) }               ---> return 80
#   - (75)[exitted] GET_MAX{[c.r][50.75.80]}:               ---> return 80
# - (50)[exitted] GET_MAX{[c.r][50.75]}:                    ---> return 80
# [RETURND] 80                                              ---> return 80

# - [exitd] while-loop: ret[75] <--- from GET_MAX{ TreeNode(75) }
# [return] ret[75]

4. PRE-order Traversal

Given binary serach tree:

          50
        /   \ 
       25     75
      /  \   /  \
    10   30 60   80

What will pre_order_traversal() print?

def pre_order_traversal(root_node: TreeNode):
    if not root_node:
        return
    print(root_node.data) 
    pre_order_traversal(root_node.left)
    pre_order_traversal(root_node.right)

4.1 PRE-order Traversal: Tony’s Guess without Python

        50
      /   \ 
     25     75
    /  \   /  \
  10   30 60   80

4.2 PRE-order Traversal: Tony’s Solution with Python

def pre_order_traversal(root_node: TreeNode):
    if not root_node:
        return
    print(root_node.data) 
    pre_order_traversal(root_node.left)
    pre_order_traversal(root_node.right)

root = TreeNode(50)
node_list = [50,25,75,10,30,60,80]
insert_from_list(root, node_list, show_results=False)
print("inorder traverse")
traverse(root)    

print()
print("preorder traversal")
pre_order_traversal(root)    

print()
print("tony expected preorder traversal")
tony_expected = [50,25,10,30,75,60,80]
[print(item) for item in tony_expected]

inorder traverse
10
25
30
50
60
75
80

preorder traversal
50
25
10
30
75
60
80

tony expected preorder traversal
50
25
10
30
75
60
80

[None, None, None, None, None, None, None]

      50
    /   \ 
   25     75
  /  \   /  \
10   30 60   80

5. POST-order Traversal

Given binary serach tree:

          50
        /   \ 
       25     75
      /  \   /  \
    10   30 60   80

What will post_order_traversal() print?

5.1 POST-order Traversal: Tony’s Guess without Python

5.2 POST-order Traversal: Tony’s Solution with Python

def post_order_traversal(root_node: TreeNode):
    if not root_node:
        return
    post_order_traversal(root_node.left)
    post_order_traversal(root_node.right)
    print(root_node.data) 

root = TreeNode(50)
node_list = [50,25,75,10,30,60,80]
insert_from_list(root, node_list, show_results=False)
print("inorder traverse")
traverse(root)    

print()
print("post_order traversal")
post_order_traversal(root)    

print()
print("tony expected post_order traversal")
tony_expected = [10,30,25,60,80,75,50]
for value in tony_expected:
    print(value)

inorder traverse
10
25
30
50
60
75
80

post_order traversal
10
30
25
60
80
75
50

tony expected post_order traversal
10
30
25
60
80
75
50

1. Draw a BST

1.1 Draw a BST: Tony’s Solution

2. Search: BST

2.1 Search: BST - Tony’s Solution

3. max() Value in BST - Tony’s Solution

3.1. TreeNode & insert_node: Setup

3.2 traverse()

3.3 find_max() Value in BST - Tony’s Solution

3.4 find_max() Version 2 - Tony’s Solution