class TreeNode():
def __init__(self,data,left=None,right=None):
self.data=data
self.left=left
self.right=right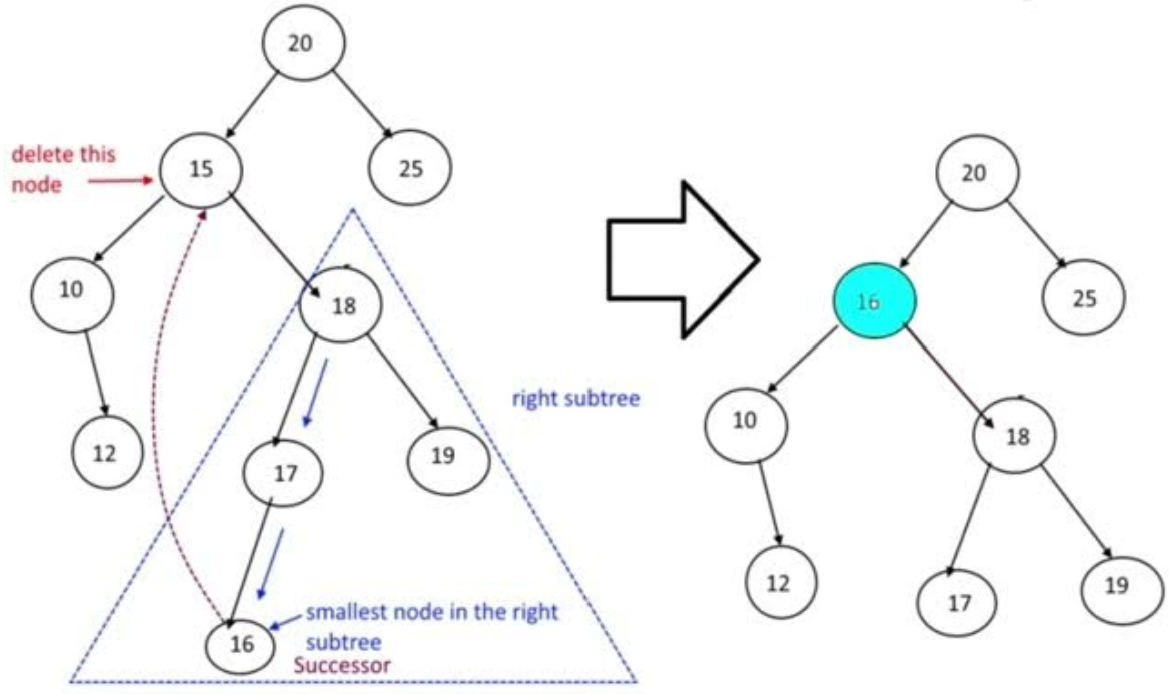
1. delete_node Again! (ETA: A very long time)
2. TreeNode() class
3. insert_node() & insert_node_list() methods
def insert_node(root_node: TreeNode, target: int):
current_node = root_node
if target == current_node.data:
print(f"Cant insert duplicates: t{target}c{current_node.data}")
return
if target < current_node.data: # go left
if current_node.left:
print(f"t{target}<-c{current_node.data}: going left...")
current_node = current_node.left
return insert_node(current_node, target)
else:
# insert left
current_node.left = TreeNode(target)
print(f"t{target}<-c{current_node.data}: inserted left of c{current_node.data} at cl{current_node.left.data}",end="\n\n")
return current_node.left
else:
if current_node.right:
print(f"t{target}->c{current_node.data}: going left...")
current_node = current_node.right
return insert_node(current_node, target)
else:
# insert right
current_node.right = TreeNode(target)
print(f"t{target}->c{current_node.data}: inserted right of c{current_node.data} at cl{current_node.right.data}",end="\n\n")
return current_node.right
def insert_node_clean2(root_node: TreeNode, target: int):
current_node = root_node
if target == current_node.data:
print(f"Cant insert duplicates: t{target}c{current_node.data}")
return
if target < current_node.data: # go left
if current_node.left:
# print(f"t{target}<-c{current_node.data}: going left...")
current_node = current_node.left
return insert_node_clean2(current_node, target)
else:
# insert left
current_node.left = TreeNode(target)
# print(f"t{target}<-c{current_node.data}: inserted left of c{current_node.data} at cl{current_node.left.data}",end="\n\n")
return current_node.left
else:
if current_node.right:
# print(f"t{target}->c{current_node.data}: going left...")
current_node = current_node.right
return insert_node_clean2(current_node, target)
else:
# insert right
current_node.right = TreeNode(target)
# print(f"t{target}->c{current_node.data}: inserted right of c{current_node.data} at cl{current_node.right.data}",end="\n\n")
return current_node.right
def insert_node_list(root: TreeNode, node_list: list[int], show_results: bool=False):
for node_int in node_list:
if show_results:
insert_node(root, node_int)
else:
insert_node_clean2(root, node_int)4. traverse() method
def traverse(root: TreeNode):
if not root:
return
traverse(root.left)
print(root.data)
traverse(root.right)5. find_successor_node() method
5.1 Psuedo-Code Scenarios Only
def find_succ_node(target_node):
print(f"t{target_node.data} has two kids[{target_node.left.data}][{target_node.right.data}]!...Find the successor child!")
# Target has 2 kids: Determine s_node to replace t_node
successor_node = target_node.right # because must be at least greater than target
# [Case_1] @[t.r]: [s_node] has {0 left-child}, [s_node] replaces [t_node]
# i. FIND S_SNODE:
# [50]t - target to delete
# X [75]s - current [s_node]
# ii. REPLACE T_NODE:
# [75]s - [target] <- [s_node]
# X []
# iii. LOGIC CHECK: is it next number after target in tree if in sequential order?
# [Case_2] @[t.r...l]: [s_node] has {a left-child}, go to {left-most-child}
# [s_node] is now {left-most-child} of {target.right}
# [50]t - [target] to delete
# X [75]s - prev [s_node] (target.right)
# [70]l...
# [60]l... - new [s_node] (left-most-child of target.right)
# [Case_2A] @[t.r...l]: [s_node] has no {right-child}
# i. FIND S_NODE:
# [50]t - [target] to delete
# X [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is currently s_node}
# [60]s... - current [s_node] (left-most-child of target.right)
# [] [] - [s_node] has no kids
# ii. REPLACE T_NODE:
# [60]s - [target] <- s_node
# X [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is None} now!
# []...
# iii. LOGIC CHECK: is it next number after target in tree if in sequential order?
# [Case_2B] @[t.r...l]: [s_node] has a {right-child}
# i. FIND S_NODE:
# [50]t - [target] to delete
# X [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is currently s_node}
# [60]s... - current [s_node] (left-most-child of target.right)
# [] [65]sr - [s_node] has a [right-child]
# ii. REPLACE T_NODE:
# [60]s - [target] <- s_node
# X [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is 65 (s_node.right)}
# [65]sr... - {s_node.right} replaces {s_node}
# iii. LOGIC CHECK: is it next number after target in tree if in sequential order?
target_node = s_node
return s_node5.2 The Code
def find_succ_node_final(t_node):
print(f"t{t_node.data} has two kids[{t_node.left.data}][{t_node.right.data}]!...Find the successor child!")
# Target has 2 kids: Determine s_node to replace t_node
s_node = t_node.right # because must be at least greater than target
# [Case_1] @[t.r]: [s_node] has {0 left-child}, [s_node] replaces [t_node]
if not s_node.left:
# i. FIND S_SNODE:
# [50]t - target to delete
# X [75]s - current [s_node]
# ii. REPLACE T_NODE:
# [75]s - [target] <- [s_node]
# X []
# s_node = t_node
print(f"[1]s_node[{s_node.data}] is our successor node!! will replace target_node[{t_node.data}]")
t_node.data = s_node.data
t_node.right = None
# iii. LOGIC CHECK: is it next number after target in tree if in sequential order?
return
# [Case_2] @[t.r...l]: [s_node] has {a left-child}, go to {left-most-child}
while s_node.left:
print(f"[2]s{s_node.data} has left_child[{s_node.left.data}]: keep going left...!")
# [s_node] is now {left-most-child} of {target.right}
# [50]t - [target] to delete
# X [75]s - prev [s_node] (target.right)
# [70]l...
# [60]l... - new [s_node] (left-most-child of target.right)
parent_node = s_node
s_node = s_node.left
# [Case_2A] @[t.r...l]: [s_node] has no {right-child}
# i. FIND S_NODE:
# [50]t - [target] to delete
# X [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is currently s_node}
# [60]s... - current [s_node] (left-most-child of target.right)
# [] [] - [s_node] has right kids (and left thats alwyays cause we went the most left already)
# ii. REPLACE T_NODE:
if not s_node.right:
print(f"[2A]s{s_node.data} has NO right child: p.left[{parent_node.left.data}] to None")
# [60]s - [target] <- s_node
# X [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is None} now!
# []...
parent_node.left = None
# iii. LOGIC CHECK: is it next number after target in tree if in sequential order?
# [Case_2B] @[t.r...l]: [s_node] has a {right-child}
# i. FIND S_NODE:
elif s_node.right:
print(f"[2B]s{s_node.data} has a right child: p.left[{parent_node.left.data}] to [{s_node.right.data}]")
parent_node.left = s_node.right
# [50]t - [target] to delete
# X [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is currently s_node}
# [60]s... - current [s_node] (left-most-child of target.right)
# [] [65]sr - [s_node] has a [right-child]
# [] [a] [b]
# ii. REPLACE T_NODE:
# [60]s - [target] <- s_node
# X [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is 65 (s_node.right)}
# [65]sr... - {s_node.right} replaces {s_node}
# iii. LOGIC CHECK: is it next number after target in tree if in sequential order?
print(f"[3]s_node[{s_node.data}] is our successor node!! will replace target_node[{t_node.data}]")
t_node.data = s_node.data
return6. delete_node() method
def delete_node_final(root_node: TreeNode, target: int):
current_node = root_node
target_node = None
parent_node = None
### ----------------------------------- A. SEARCH ----------------------------------- ###
while current_node:
if target == current_node.data:
target_node = current_node # t_node & c_node both point to target
print(f"t{target}c{current_node.data}: t_node{target_node.data} found, determine kids...")
break
elif target < current_node.data: # go left
parent_node = current_node
current_node = current_node.left
else:
parent_node = current_node
current_node = current_node.right
if not target_node:
print(f"{target} not found!")
return
# print("WTF")
### ----------------------------------- B. DELETE ----------------------------------- ###
### ----- I. 2 KIDS ----- ###
if target_node.left and target_node.right:
find_succ_node_final(target_node)
return
else:
# root node: no parents
targets_child_node = (target_node.left or target_node.right)
if not parent_node:
root_node.data = targets_child_node.data # 50->25 cn and tn points
### ADD LOGIC: if Tchild.left or Tchild.right exists: assign
root_node.left = targets_child_node.left
root_node.right = targets_child_node.right
# [] no p - root
# [50]t | [25]c
# [25]c | {10} {15}
# 10 15 |
return
elif parent_node.left == target_node: # target is non-root, left of parent
parent_node.left = targets_child_node
# [45]p or p
# [40]t | or p.left -> p.left=t.child
# [25]c | or t.child
# 10 15 |
return
elif parent_node.right == target_node: # target is non-root, right of parent
parent_node.right = targets_child_node
return
return# [Case_1] @[t.r]: [s_node] has {0 left-child}, [s_node] replaces [t_node]
# i. FIND S_SNODE:
# [50]t - target to delete
# 25 [75]s - current [s_node]
# ii. REPLACE T_NODE:
# [75]s - [target] <- [s_node]
# 25 []
# iii. LOGIC CHECK: is it next number after target in tree if in sequential order?
root = TreeNode(50)
node_list = [25,75]
insert_node_list(root, node_list)
traverse(root) # 25,75
print()
delete_node_final(root, 50)
print()
print("expected: 25,75")
traverse(root) # 25,75
print()
print(f"{root.data},75")
print(f"{root.left.data},25")
# print(root.right.data)25
50
75
t50c50: t_node50 found, determine kids...
t50 has two kids[25][75]!...Find the successor child!
[1]s_node[75] is our successor node!! will replace target_node[50]
expected: 25,75
25
75
75,75
25,25 # [Case_2] @[t.r...l]: [s_node] has {a left-child}, go to {left-most-child}
# [s_node] is now {left-most-child} of {target.right}
# [50]t - [target] to delete
# 25 [75]s - prev [s_node] (target.right)
# [70]l...
# [60]l... - new [s_node] (left-most-child of target.right)
# [Case_2A] @[t.r...l]: [s_node] has no {right-child}
# i. FIND S_NODE:
# [50]t - [target] to delete
# 25 [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is currently s_node}
# [60]s... - current [s_node] (left-most-child of target.right)
# [] [] - [s_node] has right kids (and left thats alwyays cause we went the most left already)
# ii. REPLACE T_NODE:
# [60]s - [target] <- s_node
# 25 [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is None} now!
# []...
# iii. LOGIC CHECK: is it next number after target in tree if in sequential order?
root = TreeNode(50)
node_list = [25,75,70,60]
insert_node_list(root, node_list)
traverse(root) # 25,50,60,70,75
print()
delete_node_final(root, 50)
print()
print("expected: 25,60,70,75")
traverse(root) # 25,60,70,75
print()
print(f"{root.data},60") #
print(f"{root.left.data},25")
print(f"{root.right.data},75")
print(f"{root.right.left.data},70")
25
50
60
70
75
t50c50: t_node50 found, determine kids...
t50 has two kids[25][75]!...Find the successor child!
[2]s75 has left_child[70]: keep going left...!
[2]s70 has left_child[60]: keep going left...!
[2A]s60 has NO right child: p.left[60] to None
[3]s_node[60] is our successor node!! will replace target_node[50]
expected: 25,60,70,75
25
60
70
75
60,60
25,25
75,75
70,70 # [Case_2B] @[t.r...l]: [s_node] has a {right-child}
# i. FIND S_NODE:
# [50]t - [target] to delete
# 25 [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is currently s_node}
# [60]s... - current [s_node] (left-most-child of target.right)
# [] [65]sr - [s_node] has a [right-child]
# ii. REPLACE T_NODE:
# [60]s - [target] <- s_node
# 25 [75] - prev [s_node] (target.right)
# [70]p... - {parent.left is 65 (s_node.right)}
# [65]sr... - {s_node.right} replaces {s_node}
# iii. LOGIC CHECK: - is it next number after target in tree if in sequential order?
root = TreeNode(50)
node_list = [25,75,70,60,65]
insert_node_list(root, node_list)
traverse(root) # 25,50,60,70,75
print()
delete_node_final(root, 50)
print()
print("expected: 25,60,65,70,75")
traverse(root) # 25,60,65,70,75
print()
print(f"{root.data},60") #
print(f"{root.left.data},25")
print(f"{root.right.data},75")
print(f"{root.right.left.data},70")
print(f"{root.right.left.left.data},65")
25
50
60
65
70
75
t50c50: t_node50 found, determine kids...
t50 has two kids[25][75]!...Find the successor child!
[2]s75 has left_child[70]: keep going left...!
[2]s70 has left_child[60]: keep going left...!
[2B]s60 has a right child: p.left[60] to [65]
[3]s_node[60] is our successor node!! will replace target_node[50]
expected: 25,60,65,70,75
25
60
65
70
75
60,60
25,25
75,75
70,70
65,65