def max_val(arr):
if len(arr)==1:
return arr[0]
if arr[0]>max_val(arr[1:]):
return arr[0]
return max_val(arr[1:])
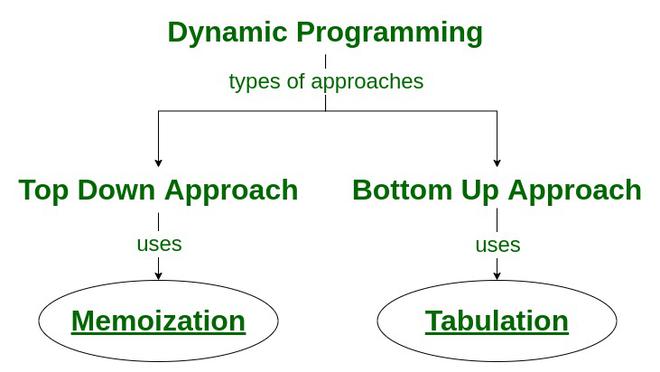
max_val([1,8,5,7,3,6])8Tony Phung
February 12, 2025
print()Without any dynamic programming techniques, the function runs uncessarily slow:
max_val_no_dp(4) is called 14-times!def max_val_no_dp(arr):
print(f"max_val_no_dp called on: {arr}")
if len(arr)==1:
return arr[0]
if arr[0]>max_val_no_dp(arr[1:]):
return arr[0]
return max_val_no_dp(arr[1:])
max_val_no_dp([1,2,3,4])max_val_no_dp called on: [1, 2, 3, 4]
max_val_no_dp called on: [2, 3, 4]
max_val_no_dp called on: [3, 4]
max_val_no_dp called on: [4]
max_val_no_dp called on: [4]
max_val_no_dp called on: [3, 4]
max_val_no_dp called on: [4]
max_val_no_dp called on: [4]
max_val_no_dp called on: [2, 3, 4]
max_val_no_dp called on: [3, 4]
max_val_no_dp called on: [4]
max_val_no_dp called on: [4]
max_val_no_dp called on: [3, 4]
max_val_no_dp called on: [4]
max_val_no_dp called on: [4]4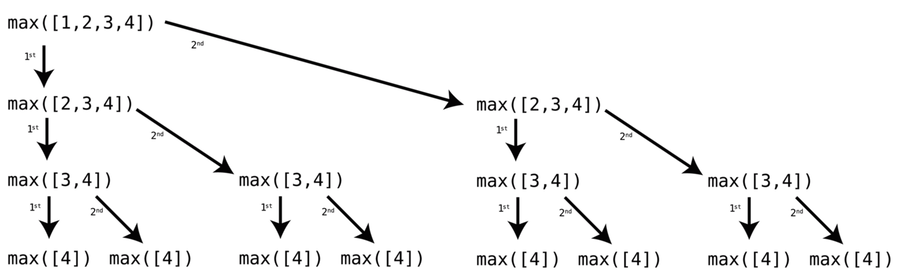
By setting the most recent call of max_val_memo to a variable max_val_remainder:
O(1)max_val_memo(4) is called 4-times onlyThis is a variation of the Dynamic Programming technique called Memoization!
By using memoization, our time-complexity reduced from:
Amazing 🥂!
def max_val_memo(arr):
print(f"max_val_memo called on: {arr}")
if len(arr)==1:
return arr[0]
max_val_remainder = max_val_memo(arr[1:])
# if arr[0]>max_val_memo(arr[1:]):
if arr[0]>max_val_remainder:
return arr[0]
return max_val_remainder
max_val_memo([1,2,3,4])max_val_memo called on: [1, 2, 3, 4]
max_val_memo called on: [2, 3, 4]
max_val_memo called on: [3, 4]
max_val_memo called on: [4]4