1. Array Operations: Exercises
For an array \(Arr[n_1,..n_{100}]\) containing \(100\) elements.
Provide the number_of_steps for the operation:
- \(Reading()\)
- \(Searching()\)
targetnot in thearray - \(Insertion()\) at \([beginning]\)
- \(Insertion()\) at \([end]\)
- \(Deletion()\) at \([beginning]\)
- \(Deletion()\) at \([end]\)
of the array.
1.1 Array Operations: Tony’s Solutions
Operation on array \(\{a_i\}^{100}_{i=1}\) |
Big \(O(n)\) | number_of_steps |
Comments |
|---|---|---|---|
\(Reading()\) any position in the array |
\(O(1)\) | \(O(1)=1\) steps | - Reading an array is like having a numpad and pressing/accessing the number required at the time needed. - No requirement count up to a particular number, we can see all numbers at once. |
\(Searching()\) target not in the array |
\(O(n)\) | \(O(100)=100\) steps | - Search (or iterate) through whole array - i.e. every single item is read once and checked against a target - It could be argued that \(Comparison()\) is an operation though but here we do not consider it as one. |
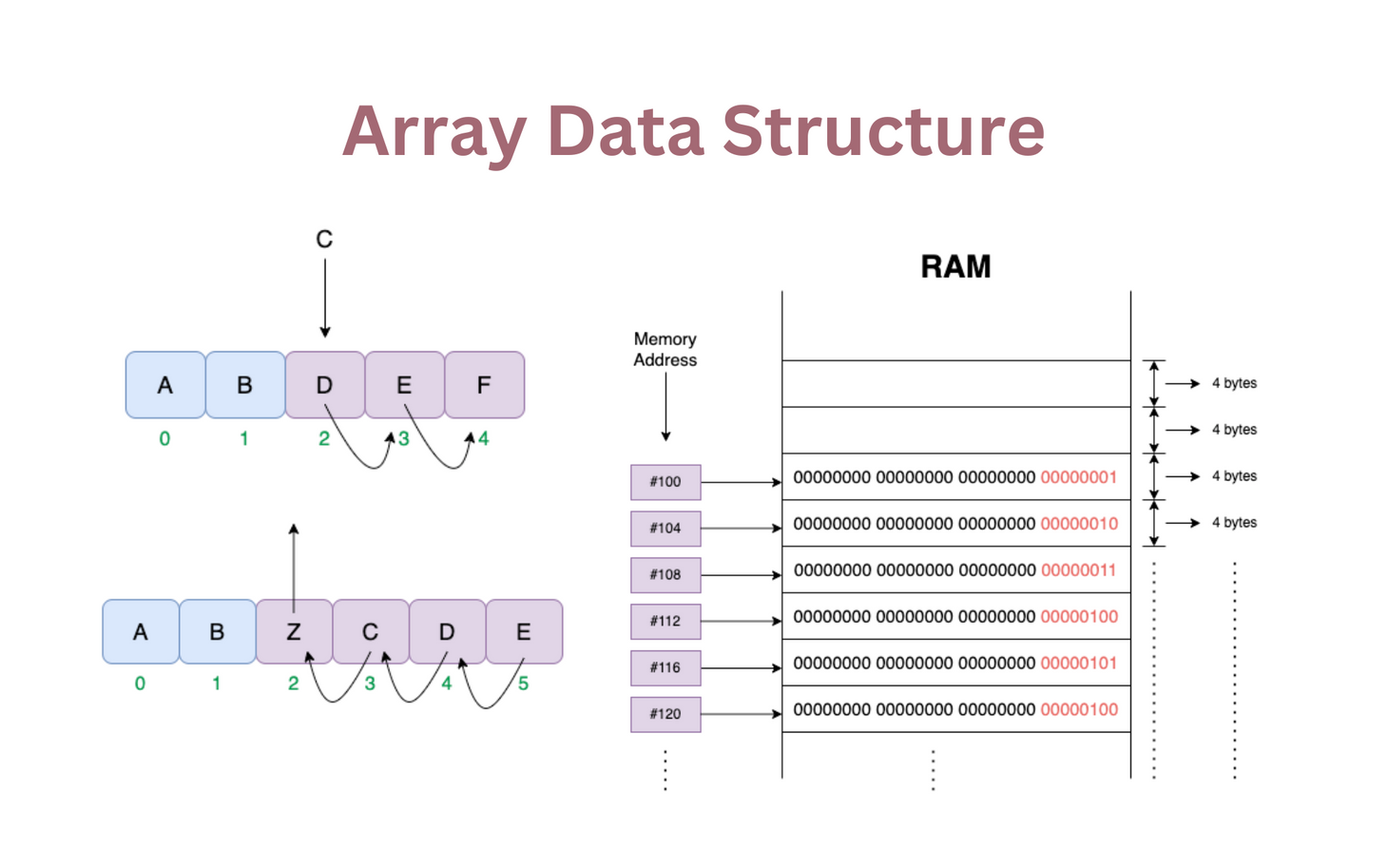
| \(Insertion()\) at \([beginning]\) | \(O(n+1)\) | \(O(101+1)=101\) steps | - \(Move()\) each item right by one - \(Move()\) last item \(Arr[n] \to Arr[n+1]\) - \(Move()\) \(2nd\_last\) item to last \(Arr[n+1] \to Arr[n],\ ...etc\) - After \(MovingAll()\) items \(\to\) \(n\) operations - \(Insert()\) value into array in \(1\ step\) - \(Total=100+1=101\ steps\) |
| \(Insertion()\) at \([end]\) | \(O(1)\) | \(O(1)=1\) steps | - Go to end of array and \(Insert()\) value in \(1\ step\) |
| \(Deletion()\) at \([beginning]\) | \(O(n)\) | \(O(99+1)=100\) steps | - \(Delete()\) \([first]\) item in $1 step - This leaves \((n-1)\) items left in the array - Move each item right by 1 - Thus, \(Arr[1] \to Arr[0],\ Arr[2] \to Arr[1]...etc...(n-1)\ times\) - \(Total=1+99=100\ steps\) |
| \(Deletion()\) at \([end]\) | \(O(1)\) | \(O(1)=1\) steps | - \(Delete()\) \([last]\) item in \(1\ step\) |
2. Array-Based Set Operations
For an array-based set \(Set\{n_1,..n_{100}\}\) containing \(100\) elements.
Provide the number_of_steps for the operation:
- \(Reading()\)
- \(Searching()\)
targetnot inset - \(Insertion()\)
new_valueat \([beginning]\) - \(Insertion()\)
new_valueat \([end]\) - \(Deletion()\) at \([beginning]\)
- \(Deletion()\) at \([end]\)
of the set.
2.1 Array-Based Set Operations: Tony’s Solutions
Operation on set \(\{a_i\}^{100}_{i=1}\) |
Big \(O(n)\) | number_of_steps |
Comments |
|---|---|---|---|
\(Reading()\) any position in the set |
\(O(1)\) | \(O(1)\) | - Same as array |
\(Searching()\) target not in the set |
\(O(n)\) | \(O(100)\) | - Same as array |
| \(Insertion()\) at \([beginning]\) | \(O(n+1)\) | \(O(2*100+1)=O(201)\) | - Search whole array: \(100\ steps\) - \(Move()\ or\ Shift()\) items right from \(Set{0} \to Set{1}, Set{1} \to Set{2}...\) (Same as array): \(100\ steps\)- \(Insert()\): \(1\ step\) - \(Search(100)\) + \(Move(100)\) + \(Insert(1)\) = \(201\ steps\) |
| \(Insertion()\) at \([end]\) | \(O(n+1)\) | \(O(100+1)=O(101)\) | - \(Search(100)\) then \(Insert(1)\) =\(101\ steps\) |
| \(Deletion()\) at \([beginning]\) | \(O(n)\) | \(O(n)\) | - \(Delete(1)\) then \(ShiftLeft(99)\) = \(100\ steps\) |
| \(Deletion()\) at \([end]\) | \(O(1)\) | \(O(1)\) | - \(Delete(1)\)=\(1\ steps\) |
3. \(Search()\) vs \(Count()\) In Arrays: Exercises
\(Search()\):
- Finds the \(first\ instance\) of a \(given\_value\) in an array.
\(Count()\):
- How many steps to find all the target_value (\(every\ instance\) of a \(given\_value\)). Give your answer \(N\).
3.1 \(Search()\) vs \(Count()\) In Arrays: Tony’s Solutions
Operation on array \(\{a_i\}^{n}_{i=1}\) |
Big \(O(n)\) | number_of_steps |
Comments |
|---|---|---|---|
\(Count()\) target_value in array |
\(O(n)\) | \(O(1)=1\) steps | - \(Search(n)\) whole array - Increase \(Counter()\) by 1 each time an occurence of target_value is seen |